22a Lesson - Non-diatonic scales

Class discussion

How do we remember modes?

Intervallic patterns: whole and half steps

Modes as they relate to major scales: What key does this mode belong to? G phrygian is the notes of Eb major in a different order.

Solfege! See how modes are altered from their relative major. G phrygian has b2, b3, b6, and b7 so you can start with G major and alter pitches from there. Major: Do, re, me, fa, sol, la, ti, do Phrygian: Do, ra, me, fa, sol, le, te, Do.

Where do the names 3+1 hexatonic and 1+3 hexatonic come from? Alternating minor seconds and minor thirds! Or.. 1 half step then 3 half steps.

Modes

Modes use every tone in a 7 degree scale.

As a review, our modes are ionian (major), dorian, phrygian, lydian, mixolydian, aeolian (natural minor), locrian.

Ionian (major) is 1234567 (Do Re Mi Fa Sol La Ti).

Dorian is 12b3456b7 (Do Re Me Fa Sol La Te).

Phrygian is 1b2b345b6b7 (Do Ra Me Fa Sol Le Te).

Lydian is 123#4567 (Do Re Me Fi Sol La Ti).

Mixolydian is 123456b7 (Do Re Mi Fa Sol La Te).

Aeolian (natural minor) is 12b345b6b7 (Do Re Me Fa Sol Le Te).

Locrian is 1b2b34b5b6b7. (Do Ra Me Fa Se Le Te).

Mixolydian is related to major because of the 3rd scale degree. Dorian is related to minor because of the b3rd scale degree.

Another common scale is Lydian Dominant 123#456b7 (Do Re Mi Fi Sol La Te).

The lydian title comes from the #4 in the first tetra scale. The dominant title comes from the b7 in the second tetra scale.

Can you hear the mode change of happy birthday?

Dorian: distinctive because of the b3 and b7. Phrygian: distinctive because of the minor tonality and b2. Lydian: almost major, but with a #4. Locrian: almost loses tonality because of the b5.

Non-Diatonic Scales

Non-Diatonic scales use more or less note names depending on the size.

There are many different types of non-diatonic scales:

1. Pentatonic (5 notes)
2. Hexatonic (6 notes)
3. Octatonic (8 notes not including repeated doh)

Pentatonic Scales

1. Major Pentatonic: 12356 (Do Re Mi Sol La).
2. Minor Pentatonic: 1b345b7 (Do Me Fa Sol Te).
   • like a Major Pentatonic if you started on La.
3. Hirajoshi: 12b35b6 (Do Re Me Sol Le).
   • like a Major Pentatonic with minor scale qualities (Me & Le).

Hextonic Scales

1. Whole Tone Scale: a pattern of whole tones, and cannot be explained in solfege or scale degrees. Ex: CDEF#G#A#, C#D#FGAB. there are only two piano patterns for a whole tone scale no matter what note you start on or how your enharmonically spell it.
2. Half-Step Minor Third (3+1): a pattern of a minor third followed by a half-step. Ex: CEbEGAbB. Half-Step Minor Third (1+3): a pattern of a half-step followed by a minor third. Ex: CDbEFAbA.

Octatonic Scales

1. Half-Whole Octatonic: a pattern of alternating half-steps and whole-steps. Ex: CDbEbEGbGABb.
2. Whole-Half Octatonic: a pattern of alternating whole-steps and half-steps. Ex: CDEbFGbAbAB.

Further reading

From Open Music Theory

Folk, pop, classical, and modern composers often organize pitch materials using scales other than major and minor. Some of these scales, like the various diatonic modes and the pentatonic collection, are relatively familiar to most listeners. Others — such as octatonic, whole-tone, and acoustic collections/scales — are more novel, and usually (but not always) found in twentieth- and twenty-first-century compositions.

When characterizing many of these new musical resources, the word “collection” is often more appropriate than “scale.” A collection is a group of notes — usually five or more. Imagine a collection as a source from which a composer can draw musical material — a kind of “soup” within which pitch-classes float freely. Collections by themselves do not imply a tonal center. But in a composition a composer may establish a tonal center by privileging one note of the collection, which we then call a scale.

Diatonic Collection (modes)

The diatonic collection is any transposition of the 7 white keys on the piano. Refer to these collections by the number of sharps and flats they contain: the “0-sharp” collection, the “1-sharp” collection, and so on. The “2-flat” collection, for example, contains the pitch classes {F, G, A, B-flat, C, D, E-flat}.

When these collections gain a tonic note, they morph into scales, which by tradition we name according to the “modal” system established in centuries ago. (Note that while these modes share their names with the modes of the Medieval Christian church, they function quite differently. The similarity is principally one of name.)

One way to look at these “modes” is to think of the seven white keys of the piano {C, D, E, F, A, B}. These notes, when starting on different pitches, create the different modal scales. By taking each note of the seven-white-key collection, and treating it as as the tonic, all seven modal scales can be played. Ionian treats C as tonic, Dorian treats D as tonic, Phrygian treats E as tonic, Lydian treats F as tonic, Mixolydian treats G as tonic, Aeolian treats A as tonic, and Locrian treats B as tonic:

Ionian mode (major scale): do re mi fa sol la ti do

Dorian mode: do re me fa sol la te do

Phrygian mode: do ra me fa sol le te do

Lydian mode: do re mi fi sol la ti do

Mixolydian mode: do re mi fa sol la te do

Aeolian mode (natural-minor scale): do re me fa sol le te do

Locrian mode (uncommon outside jazz): do ra me fa se le te do

Like the major and minor scales, these intervallic relationships can be transposed to any tonic pitch.

Pentatonic Collection

Pentatonic collections are five-note subsets of the diatonic collection. Here’s a quick way to create a pentatonic collection: (1) List the notes of a major scale. (2) Remove scale degress 4 and 7. (E.g., the pentatonic collection {C,D,E,G,A} corresponds to scale degrees 1,2,3,5,6 of the C major scale.)

Removing scale degrees 4 and 7 results in a collection with no half steps. As a result of its “halfsteplessness”, any member of the collection easily functions as a tonal center. For example, given the 0-sharp pentatonic collection, there are five unique scales formed when each of the collection’s pitch classes become a tonic: C pentatonic (C,D,E,G,A), D pentatonic (D,E,G,A,C), E pentatonic (E,G,A,C,D), and so on.

The black keys on the piano also form a pentatonic collection:

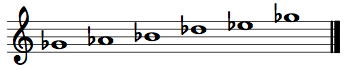
Whole Tone Collection

This is a group of notes generated entirely by whole tones: {0,2,4,6,8,10}, for example.

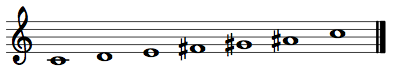
There are only two unique whole-tone collections. WT0 contains pitch classes {0,2,4,6,8,10}, while WT1 contains pitch classes {1,3,5,7,9,11}. In other words, WT0 contains the pitch classes {C, D, E, F-sharp, G-sharp, B-flat}, while WT1 contains pitch classes {C-sharp, D-sharp, F, G, A, B}.

Octatonic Collection

Called octatonic because it has eight pitch classes, the octatonic collection is full of compositional potential and has been used by many composers to a variety of ends. An octatonic collection is easily generated by alternating half steps and whole steps. Using pitch class numbers, one example is {0,1,3,4,6,7,9,10}.

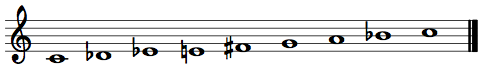
The interval content of this collection is very homogenous, and this intervallic consistency leads to one of its most interesting properties. When we transpose the above collection by 3—adding 3 to each of the integers in the collection—{0,1,3,4,6,7,9,10} becomes {3,4,6,7,9,10,0,1}. Comparing the two shows that these collections are exactly the same! In fact, you would come up with the same collection if you transposed it by 6 or 9 as well.

Olivier Messiaen called such collections “modes of limited transposition.” (The whole-tone scale is also a mode of limited transposition.) And as a result of the property, there are only three unique octatonic collections. We name these arbitrarily as OCT(0,1), OCT(1,2), and OCT(2,3). The numbers to the right of “OCT” are pitch classes within that scale. (E.g., the {0,1,3,4,6,7,9,10} collection I discussed above is OCT(1,2).) We can also call them C–C♯ octatonic, C♯–D octatonic, and D–E♭ octatonic.

Other Collections and Scales

There are many, many other collections and scales used by composers and musicians in the twentieth- and twenty-first centuries. Messiaen, for example, described five more modes of limited transposition, and there are other smaller collections that have the same property. Acoustic scales, formed from the first seven unique partials of the overtone series, are common in the music of Debussy, Bartok, and Crumb — ocassionally as a representation of nature. Jazz musicians have an entire set of scales used for improvisation. Non-Western musics often have unique systems of scales and collections, such as the rāgas used in Indian classical music.

More generally, any large set of pitch classes that form the basis for a passage may function as a collection, even if it has no familiar name. Most often, music theorists refer to these collections with pitch-class set notation.

---

This resource was created by Brian Moseley and contains contributions from Meredith Cahill, Elise Campbell, and Kris Shaffer.