22a Discussion - Non-diatonic scales

Class Discussion

Non Diatonic Scales

Whole Tone Scale A whole tone “scale” is a collection of six tones that are built entirely using whole steps. There are only two whole unique tones scales, because once you create one whole tone scale, and then move that shape up by half step, you have included all twelve tones. This is a symmetrical scale.

Mediant Harmony In western music, we are often looking at chord progressions in which the roots of the chords move down by fifths (ii, vi, ii, V, I). Mediant harmony is when chords have roots that move in thirds. In the past, we have talked about how some chords can replace other chords because the share one or more tones. For example, the IV chord can replace the II chord, the viio chord can replace the V chord, etc. This is similar to how mediant harmony works. Mediant harmony works because of smooth voice leading and resolution by step. Let’s look at the chords C and Emin. These chords share two notes (E and G) and in order to move from C to Emin using smooth voice leading, you would only need to move one note one half step (C to B).

Any chord can now move to any other chord that has a root a M3 or m3 away. For example, Bb can move to D, Dmin, Db, Dbmin, G, Gmin, Gb, and Gbmin. These are the eight “mediants” of the chord Bb. There are two diatonic mediants, which don’t need any alteration to exist in the key (Dmin and Gmin). There are four chromatic mediants: two that are the other form of the diatonic mediants (major or minor), and two that are taken from the relative minor (Db and Gb). There are also two doubly chromatic mediants, which are altered from the relative minor (Dbmin and Gbmin).

Hexatonic Scales Hexatonic scales are scales built on alternating minor thirds and half steps. There are four unique hexatonic scales - two 3+1, and two 1+3. They are similar to the whole tone scale but shifted over by a half step. Also symmetrical.

Octatonic Scales The octatonic scale is a scale built on alternating half steps and whole steps. There for there are “whole-half octatonic” scales and “half-whole octatonic” scales (often labeled WH, or HW octatonic). There are three unique octatonic scales. Because scales usually have seven unique pitches, and the octatonic scale has eight tones, it will include a diminished third.

Class discussion 2021

What is a collection?

• A collection is an organized group of pitches. It’s kind of a squares and rectangles situation. All scales are collections, but not all collections are scales.

What is a mode?

• Related to major scales, modes are based around the various scales degrees of a major scale. For example, E Phrygian is the same key signature as C major but starts on the third scale degree
  • If thinking in terms of what is altered from the original key is more helpful, you can instead think of E Phrygian as having a lowered 2, 3, 6, and 7. Each mode has its own lowered (or raised) scale degrees

Seven note collections

All our modes:

• Ionian (major)
• Dorian: 2nd degree of major scale/lowered 3 and 7
• Phrygian: 3rd degree of major scale/lowered 2, 3, 6, and 7
• Lydian: 4th degree of major scale/raised 4
• Mixolydian: 5th degree of major scale/lowered 7
• Aeolian (natural minor)
• Locrian: 7th degree of major scale/lowered 2, 3, 5, 6, and 7
• Lydian Dominant: half Lydian, half Mixolydian/raised 4, lowered 7. You can remember this scale’s relation to Mixolydian because of “dominant”/V because Mixolydian is based around the fifth scale degree

Five note collections

Major pentatonic

• 1, 2, 3, 5, 6/do re mi sol la

Minor pentatonic

• 1, b3, 4, 5, b7
• Related to the major pentatonic scale in the same way that the regular major and minor scales are related: minor pentatonic is just major pentatonic starting on la

Hirajoshi pentatonic

• 1, 2, b3, 5, b6/do re me sol le
• Major pentatonic using minor notes

Six note collections

Whole tone scale

• Every note is a whole step apart. There are only two unique whole tone collections: C D E F# G# A# and Db Eb F G A B. You can start on any of the notes within these collections, but the cycle of the two will be the same
• There’s no possible center to a whole tone scale because there are six notes in it and they are all a whole step apart. This gives it its characteristic off-kilter feeling
• Whole tone scale don’t have a standard mode of notation but will always have a diminished third somewhere
• Another way to think of these is as two interlocking augmented triads. For example, with the first whole tone collection (C D E F# G# A#), it is made up of the two augmented triads C E G# and D F# A#
• Pretty common in music because composers like to do cool and fancy stuff with them

3+1 and 1+3 Hexatonic

• Based on interval patterns. 3+1 trades off between a minor third and a half step between each note, and 1+3 trades off between a half step and a minor third between each note
• The 3 actually means three half steps, but it may be easier to think of it as a minor third instead
• These scales have 4 unique collections which you can look at in the textbook because I don’t want to write them all out here sorry
• As an example, though, each collection can be used for either scale. Starting on a note that is followed by a half step, you start a 1+3 hexatonic scale. Starting on one followed by a minor third, you start a 3+1 hexatonic scale
• We always label these scales in ascending form!! You might be asked to build a descending one of these, so make sure the interval pattern is correct

Eight note collections

Ocatonic (also called a diminished scale)

• Happen either half-whole (HW) or whole-half (WH)
• Start on one note and alternate between half and whole steps (for a HW octatonic) or between whole and half steps (for a WH octatonic)
• 3 unique octatonic collections. Just like the hexatonic and whole tone scales, you can start on any pitch within the collections to get a different scale
• Stravinsky likes these! They have the potential to sound really spooky and weird

Further reading

From Open Music Theory

Folk, pop, classical, and modern composers often organize pitch materials using scales other than major and minor. Some of these scales, like the various diatonic modes and the pentatonic collection, are relatively familiar to most listeners. Others — such as octatonic, whole-tone, and acoustic collections/scales — are more novel, and usually (but not always) found in twentieth- and twenty-first-century compositions.

When characterizing many of these new musical resources, the word “collection” is often more appropriate than “scale.” A collection is a group of notes — usually five or more. Imagine a collection as a source from which a composer can draw musical material — a kind of “soup” within which pitch-classes float freely. Collections by themselves do not imply a tonal center. But in a composition a composer may establish a tonal center by privileging one note of the collection, which we then call a scale.

Diatonic Collection (modes)

The diatonic collection is any transposition of the 7 white keys on the piano. Refer to these collections by the number of sharps and flats they contain: the “0-sharp” collection, the “1-sharp” collection, and so on. The “2-flat” collection, for example, contains the pitch classes {F, G, A, B-flat, C, D, E-flat}.

When these collections gain a tonic note, they morph into scales, which by tradition we name according to the “modal” system established in centuries ago. (Note that while these modes share their names with the modes of the Medieval Christian church, they function quite differently. The similarity is principally one of name.)

One way to look at these “modes” is to think of the seven white keys of the piano {C, D, E, F, A, B}. These notes, when starting on different pitches, create the different modal scales. By taking each note of the seven-white-key collection, and treating it as as the tonic, all seven modal scales can be played. Ionian treats C as tonic, Dorian treats D as tonic, Phrygian treats E as tonic, Lydian treats F as tonic, Mixolydian treats G as tonic, Aeolian treats A as tonic, and Locrian treats B as tonic:

Ionian mode (major scale): do re mi fa sol la ti do

Dorian mode: do re me fa sol la te do

Phrygian mode: do ra me fa sol le te do

Lydian mode: do re mi fi sol la ti do

Mixolydian mode: do re mi fa sol la te do

Aeolian mode (natural-minor scale): do re me fa sol le te do

Locrian mode (uncommon outside jazz): do ra me fa se le te do

Like the major and minor scales, these intervallic relationships can be transposed to any tonic pitch.

Pentatonic Collection

Pentatonic collections are five-note subsets of the diatonic collection. Here’s a quick way to create a pentatonic collection: (1) List the notes of a major scale. (2) Remove scale degress 4 and 7. (E.g., the pentatonic collection {C,D,E,G,A} corresponds to scale degrees 1,2,3,5,6 of the C major scale.)

Removing scale degrees 4 and 7 results in a collection with no half steps. As a result of its “halfsteplessness”, any member of the collection easily functions as a tonal center. For example, given the 0-sharp pentatonic collection, there are five unique scales formed when each of the collection’s pitch classes become a tonic: C pentatonic (C,D,E,G,A), D pentatonic (D,E,G,A,C), E pentatonic (E,G,A,C,D), and so on.

The black keys on the piano also form a pentatonic collection:

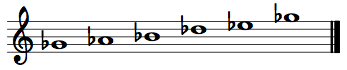
Whole Tone Collection

This is a group of notes generated entirely by whole tones: {0,2,4,6,8,10}, for example.

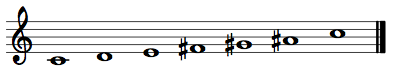
There are only two unique whole-tone collections. WT0 contains pitch classes {0,2,4,6,8,10}, while WT1 contains pitch classes {1,3,5,7,9,11}. In other words, WT0 contains the pitch classes {C, D, E, F-sharp, G-sharp, B-flat}, while WT1 contains pitch classes {C-sharp, D-sharp, F, G, A, B}.

Octatonic Collection

Called octatonic because it has eight pitch classes, the octatonic collection is full of compositional potential and has been used by many composers to a variety of ends. An octatonic collection is easily generated by alternating half steps and whole steps. Using pitch class numbers, one example is {0,1,3,4,6,7,9,10}.

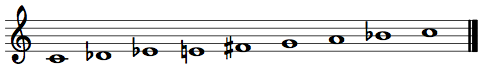
The interval content of this collection is very homogenous, and this intervallic consistency leads to one of its most interesting properties. When we transpose the above collection by 3—adding 3 to each of the integers in the collection—{0,1,3,4,6,7,9,10} becomes {3,4,6,7,9,10,0,1}. Comparing the two shows that these collections are exactly the same! In fact, you would come up with the same collection if you transposed it by 6 or 9 as well.

Olivier Messiaen called such collections “modes of limited transposition.” (The whole-tone scale is also a mode of limited transposition.) And as a result of the property, there are only three unique octatonic collections. We name these arbitrarily as OCT(0,1), OCT(1,2), and OCT(2,3). The numbers to the right of “OCT” are pitch classes within that scale. (E.g., the {0,1,3,4,6,7,9,10} collection I discussed above is OCT(1,2).) We can also call them C–C♯ octatonic, C♯–D octatonic, and D–E♭ octatonic.

Other Collections and Scales

There are many, many other collections and scales used by composers and musicians in the twentieth- and twenty-first centuries. Messiaen, for example, described five more modes of limited transposition, and there are other smaller collections that have the same property. Acoustic scales, formed from the first seven unique partials of the overtone series, are common in the music of Debussy, Bartok, and Crumb — ocassionally as a representation of nature. Jazz musicians have an entire set of scales used for improvisation. Non-Western musics often have unique systems of scales and collections, such as the rāgas used in Indian classical music.

More generally, any large set of pitch classes that form the basis for a passage may function as a collection, even if it has no familiar name. Most often, music theorists refer to these collections with pitch-class set notation.

---

This resource was created by Brian Moseley and contains contributions from Meredith Cahill, Elise Campbell, and Kris Shaffer.